Portable implementation of a computation kernel for the N-body problem with Kokkos
Table of Contents
- 1. Foreword
- 2. Introduction
- 3. Source code
- 4. Benchmarks and results
- 5. Closing remarks
- 6. References
1. Foreword
This document summarizes the work completed during Aurélien Gauthier's internship with the CONCACE team, under the supervision of Antoine Gicquel, PhD student in CONCACE. The objective was to explore the Kokkos ecosystem by attempting to implement existing kernels from the ScalFMM library. This document serves as a reflection on that experience and includes code snippets from the developed implementations to highlight some of the features offered by Kokkos. However, note that it is not intended to be a formal guide or comprehensive summary of the official documentation (which can be found here), though pointers to relevant sections are provided. We only explored specific features of Kokkos that suited our needs for a specific target application (detailed in the introduction), and thus, this document does not aim to be an exhaustive overview of the library. Nonetheless, we hope that our experience might be valuable to others interested in learning more about Kokkos. At the time of writing, the latest release of Kokkos is version 4.3.01, please note that some features presented here may change as the API evolves. Additionally, certain results are preliminary and may require further investigation (see the result section). Finally, feedback is warmly welcome!
2. Introduction
Before diving into the heart of the matter, let’s briefly introduce the context of the internship.
2.1. Context
We are interested in physical applications where we evaluate pairwise interactions between \(N\) bodies (by "bodies" we mean particles, planets, celestial objects, etc.). Each of the \(N\) bodies is located at a position \(x_i \in \mathbb{R}^n\) (\(n=2\) or \(n=3\) most of the time). Generally, this can be expressed as follows:
\begin{equation} \Phi_i = \sum_{j = 1, i \neq j}^{N}{ k(x_i, x_j)m_j} \quad \forall i \in \{1,\dots,N\}. \label{eq:n-body} \end{equation}In equation \eqref{eq:n-body}:
- \(x_i\) is the position of body \(i\).
- \(m_i\) represents the input for body \(i\) (for example, it could be an electric charge or mass).
- \(\Phi_i\) represents the output for body \(i\) (for example, it could be a potential or a force).
- \(k(x,y)\) if the interaction function (or interaction kernel). This function often has a singularity when \(x\) and \(y\) are close to each other, but it becomes smooth and decays rapidly as the distance from the singularity increases.
We will now provide some examples of this physical problem.
2.1.1. Electrostatic potential
In this case, we consider a set of \(N\) particles, each with a charge \(q_i\), and we want to compute the potential \(p_i\) for each one of them using the following expression:
\begin{equation} p_i = \frac{1}{4\pi \epsilon_0} \sum_{j = 1, i \neq j}^{N}{ \frac{q_j}{\|x_i - x_j\|} } \quad \forall i \in \{1,\dots,N\}, \label{eq:potential} \end{equation}where \(\epsilon_0\) is the vaccum permeability. Thus, the interaction function is defined as:
\begin{equation*} k(x,y) = \frac{1}{\|x - y\|}. \label{eq:potential-kernel} \end{equation*}2.1.2. Gravitational interactions
In this case, we have a set of \(N\) celestial bodies (planets, stars, etc…) each with a mass \(m_i\), and we aim to calculate the total force \(\vec{F}_i\) acting on each one of them using the following formula:
\begin{equation} \vec{F}_i = G m_i \sum_{j = 1, i \neq j}^{N}{ \frac{(x_j - x_i)}{\|x_i - x_j\|^3} m_j } \quad \forall i \in \{1,\dots,N\}, \label{eq:force} \end{equation}where \(G\) is the gravitational constant. Thus, the interaction function is defined as:
\begin{equation*} k(x,y) = \frac{x - y}{\|x - y\|^3}. \label{eq:force-kernel} \end{equation*}2.2. The Fast Mutipole Method
One can notice that the naive direct evaluation of \eqref{eq:n-body} has quadratic complexity (i.e., \(\BigO(N^2)\)). The Fast Multipole Method (FMM) (Greengard and Rokhlin 1987) is a hierarchical method used to accelerate the evaluation of \eqref{eq:n-body}. It specifically speeds up the computation of long-range interactions (i.e., the distant interactions) between a large number of bodies. Instead of calculating all pairwise interactions by evaluating \eqref{eq:n-body}, which would be obviously prohibitively time-consuming, the FMM groups distant bodies and approximates their interactions. This significantly reduces the computation time. For a more comprehensive, in-depth explanation of the FMM, we direct the reader to the first chapter of (Blanchard 2017). However, a thorough understanding of the FMM is not required to follow this document; this reference is provided simply to give the overall context.
In the FMM algorithm, the space in which the \(N\) bodies are located is hierarchically divided into clusters (or boxes) that are nested within one another. This hierarchical division is usually represented by a tree, where each node represents a box (this is a \(d\) -tree; in 3D it is called an octree, and in 2D, a quadtree,…). We usually consider that interactions between bodies located in the same box or in neighboring boxes are part of the near field, while other interactions are part of the far field.
In practice, the FMM separates the computation of the near field from the far field. As briefly mentioned above, the FMM groups distant bodies and uses approximations to compute the far field. However, for the near field calculation, approximations are not accurate enough. As a consequence, the interactions between each pair of bodies must be computed explicitly and precisely (like in expression \eqref{eq:n-body}). This is the purpose of the P2P operator, which we will describe in the next paragraph. In the end, the FMM algorithm performs a fast evaluation of \eqref{eq:n-body} (by "fast evaluation" we mean \(\BigO(N \log{N})\) and even \(\BigO(N)\) with a multi-level strategy).
2.3. The P2P kernel
As we mentioned earlier, the P2P (Particle-to-Particle) kernel is the part of the FMM algorithm responsible for the direct calculation of interactions between nearby bodies.
There are actually two variants of the P2P kernel, but the underlying concept is the same for both: iterating through bodies to update the output of others. In this context, we refer to the bodies whose outputs are being updated as target bodies, and those contributing to the interactions as source bodies. Note that, in most cases, the target and source bodies are actually the same.
- First version: The P2P inner kernel (see Algorithm 1) calculates the interactions between bodies located within the same box \(B\). We can notice that we skip the case where \(i = j\) (i.e., self-interaction). This situation corresponds to the one illustrated in Figure 2.
Figure 1: P2P inner algorithm
Figure 2: Bodies in a single box (typical situation for the P2P inner kernel)
- Second version: The P2P outer kernel (see Algorithm 3) calculates the interactions between bodies located in two neighboring boxes. We consider a first box \(B_1\) with \(M\) bodies and a second box \(B_2\) with \(N\) other bodies. Each of the bodies in \(B_1\) contributes to update the output of the bodies in \(B_2\). This situation corresponds to the one illustrated in Figure 4.
Figure 3: P2P outer algorithm
Figure 4: Bodies in neighboring boxes (typical situation for the P2P outer kernel)
From now on, without loss of generality, we will focus only on the P2P inner kernel in the case of the electrostatic potential (see \eqref{eq:potential}) in a simple two-dimensional application (i.e, \(n = 2\)). In other words, we aim to compute:
\begin{equation} p_i = \sum_{j = 1}^{N}{ \frac{q_j}{\|x_i - x_j\|} } \quad \forall i \in \{1,\dots,N\} \qquad \text{ with } x_i \in \mathbb{R}^2, \label{eq:potential-electro} \end{equation}with \(p_i\) the potential of particle \(i\) and \(q_j\) the charge of particle \(j\). This was the target kernel that we attempted to implement using Kokkos.
2.4. Kokkos in a nutshell
Before moving forward, let's provide a brief introduction to Kokkos (Trott et al. 2022; Edwards, Trott, and Sunderland 2014). It is most of the time presented as a C++ library designed for performance portability in HPC applications. It allows developers to write parallel code that runs efficiently across various hardware architectures, including CPUs and GPUs, without the need to rewrite code for each platform. By providing abstractions for parallel execution and memory management, Kokkos allows users to leverage different backends (e.g., OpenMP, CUDA) through a single, unified API. However, it is important to note that these backends must be selected at compile-time. During the internship, we tested the following backends: OpenMP (CPU), C++ threads (CPU), and CUDA (GPU). However, other backends are currently supported (such as HIP) and more are planned for the future. Last but not least, Kokkos relies on key abstractions, such as the memory space, which determines where the data is located, and the execution space, which specifies where the code is executed.
The most convenient way to install Kokkos is via CMake (but you can find other alternatives in the documentation). However, Guix also offers an easy way to switch between different backends, making it simple to configure Kokkos for various architectures. For example, the following lines can be used to create development environments via guix shell using the --pure option:
- Using OpenMP as a backend:
guix shell --pure kokkos-openmp gcc-toolchain@11 <other packages> ...
- Using C++ threads as a backend:
guix shell --pure kokkos-threads gcc-toolchain@11 <other packages> ...
- Using CUDA as a backend:
guix shell --pure kokkos-cuda-a100 gcc-toolchain@11 cuda-toolkit@12.4 <other packages> ... export LD_PRELOAD=/usr/lib64/libcuda.so:/usr/lib64/libnvidia-ptxjitcompiler.so # required to use CUDA with guix
We provide suitable Guix environments to run the implementations with these backends in the results section.
As mentioned earlier, Kokkos is written in modern C++ and makes extensive use of advanced C++ programming techniques. However, it offers a straightforward API, so users do not need to engage with complex C++ code to work with Kokkos. That said, it is still beneficial to be familiar with C++ templates. Roughly speaking, Templates allow for writing generic and reusable code that can handle different data types. They allow users to write functions and classes to be defined independently of specific types, so the same code can operate on various data types without duplication.
- A (non-exhaustive) starting point for getting a good grasp of C++ templates: Wikipedia - C++ Templates
- Entry point for templates in the reference documentation: cppreference.com - Templates
3. Source code
3.1. Baseline implementation
We begin by introducing the naive sequential implementation of the P2P inner kernel. This version serves as a baseline for the experiments and is only used to verify the numerical results. The implementation is quite basic, leaving significant room for optimization. Indeed, we can notice for example that it does not take advantage of the computation's inherent symmetry. In this approach, we simply iterate over the target particles and update their potential by calculating interactions with all source particles, while skipping self-interactions (we remind the reader that, in that case, the target and source particles are actually the same).
#pragma once #include "utils.hpp" #include <concepts> #include <iostream> #include <vector> /** * @brief Naive version of the P2P inner kernel. * * This function calculates pairwise interactions (potential in this case) between particles based on * their positions and charges. It iterates over all target particles and computes their interaction * with all source particles, except themselves, and stores the result in the `potential` array. * * @tparam ContainerType The type of container used for the positions, charges, and potentials. This container must * support random access (e.g., `std::vector`, `std::array`) and store floating-point values. * * @param[in] position_x Container of x-coordinates of the particles. * @param[in] position_y Container of y-coordinates of the particles. * @param[in] charge Container of charge values associated with each particle. * @param[out] potential Output container where the computed potential for each particle is stored. * */ template<Container ContainerType> auto simplified_p2p_inner(ContainerType const& position_x, ContainerType const& position_y, ContainerType const& charge, ContainerType& potential) -> void { // set-up (aliases) using container_type = ContainerType; using value_type = typename container_type::value_type; const std::size_t size = position_x.size(); value_type result; // loop through the target data for(std::size_t i = 0; i < size; ++i) { const value_type local_x_target = position_x[i], local_y_target = position_y[i]; result = 0.; // loop through the source data (we skip the case where 'i == j') for(std::size_t j = 0; j < i; ++j) { const value_type diff_y = position_y[j] - local_y_target, diff_x = position_x[j] - local_x_target; result += charge[j] / std::sqrt(diff_y * diff_y + diff_x * diff_x); } for(std::size_t j = i + 1; j < size; ++j) { const value_type diff_y = position_y[j] - local_y_target, diff_x = position_x[j] - local_x_target; result += charge[j] / std::sqrt(diff_y * diff_y + diff_x * diff_x); } // update potential potential[i] = result; } }
3.2. Existing implementations
Prior to the internship, there were existing implementations of the P2P inner kernel, which were originally more generic but had been adapted to the simplified two-dimensional case. These included a CPU vectorized version using xsimd and a CUDA version. We begin by presenting these two versions, as they will serve as a baseline for comparison with the Kokkos-based implementations.
3.2.1. Implementation on CPU using xsimd
This implementation is a simplified version of a kernel extracted from ScalFMM 3.0 and was adapted for this simplified context (the two-dimensional case). It leverages the xsimd C++ library which provides wrappers for SIMD intrinsics. Roughly speaking, the xsimd library automatically detects and uses the available SIMD instruction sets on the target machine, for instance SSE, AVX, AVX2, and AVX512 on x86 architectures, and NEON on ARM architectures (an exhaustive list of the supported instruction sets is given in their documentation). One of the key benefits of using xsimd is its portability; it offers a high-level API that can be used across different CPU architectures, simplifying the process of writing SIMD-optimized code without having to handle specific low-level instruction sets (have a look at the Intel instrinsics guide to see how cumbersome it can be to use it manually, especially for beginners). This library relies on SIMD instruction detection at compile-time, allowing the same code to adapt to different target architectures. Another consequence is that these wrappers don't introduce any runtime overhead compared to the use of raw instrinsics. Additionally, xsimd is tightly integrated with xtensor, a Numpy-like multidimensional array library for C++, which provides excellent tools for scientific computing. In the implementation below, we vectorize the first part of the outermost loop (over the target data) by using SIMD batches to process multiple particles simultaneously, while the remaining part of the loop is treated in the "standard scalar manner". To remove self-interactions, we use SIMD batch logical masks, which act as filters to exclude them efficiently.
#pragma once #include "utils.hpp" #include <concepts> #include <iostream> #include <type_traits> #include <xsimd/xsimd.hpp> // Helper function to print the SIMD instruction set being used void print_simd_instruction_set() { std::cout << "- SIMD instruction set: "; #if XSIMD_WITH_AVX512F std::cout << "AVX-512" << '\n'; #elif XSIMD_WITH_AVX2 std::cout << "AVX2" << '\n'; #elif XSIMD_WITH_AVX std::cout << "AVX" << '\n'; #elif XSIMD_WITH_SSE4_2 std::cout << "SSE4.2" << '\n'; #elif XSIMD_WITH_SSE4_1 std::cout << "SSE4.1" << '\n'; #elif XSIMD_WITH_SSE2 std::cout << "SSE2" << '\n'; #elif XSIMD_WITH_NEON std::cout << "NEON" << '\n'; #else std::cout << "Unknown SIMD instruction set \n"; #endif } /** * @brief P2P inner kernel using SIMD vectorization via xsimd. * * This function calculates pairwise interactions (potential in this case) between particles based * on their positions and charges. It leverages SIMD vectorization via the **xsimd** library to * process multiple particles simultaneously. The function uses SIMD to handle large portions of the * data in parallel, while a scalar fallback handles any remaining particles that don't fit into a full * SIMD batch. We use SIMD batch logical masks to remove self-interactions (acting as a filter). * * @tparam ContainerType The type of container used for the positions, charges, and potentials. This container must * support random access (e.g., `std::vector`, `std::array`) and store floating-point values. * * @param[in] position_x Container of x-coordinates of the particles. * @param[in] position_y Container of y-coordinates of the particles. * @param[in] charge Container of charge values associated with each particle. * @param[out] potential Output container where the computed potential for each particle is stored. * */ template<Container ContainerType> auto p2p_inner_xsimd(ContainerType const& position_x, ContainerType const& position_y, ContainerType const& charge, ContainerType& potential) -> void { // Set-up (aliases) using container_type = ContainerType; using value_type = typename container_type::value_type; using batch_type = xsimd::batch<value_type>; static constexpr std::size_t batch_size = batch_type::size; const std::size_t size = position_x.size(); const std::size_t vec_size = size - size % batch_size; const value_type local_tolerance{std::numeric_limits<value_type>::epsilon()}; batch_type vec_contribution; // Initialize logical mask std::array<value_type, batch_size> next_target_indices; std::iota(next_target_indices.begin(), next_target_indices.end(), value_type(0.)); auto vec_next_target_indices = xsimd::load_unaligned(next_target_indices.data()); // Loop through target data (vectorized part) for(std::size_t i = 0; i < vec_size; i += batch_size, vec_next_target_indices += batch_size) { const batch_type vec_local_target_x = xsimd::load_unaligned(&position_x[i]); const batch_type vec_local_target_y = xsimd::load_unaligned(&position_y[i]); vec_contribution = 0.; // Loop through source data for(std::size_t j = 0; j < size; ++j) { const batch_type vec_diff_x = vec_local_target_x - position_x[j], vec_diff_y = vec_local_target_y - position_y[j]; // Apply logical mask to skip the case 'i = j' const auto batch_mask = xsimd::abs(vec_next_target_indices - j) > local_tolerance; vec_contribution += xsimd::select( batch_mask, charge[j] / xsimd::sqrt(vec_diff_x * vec_diff_x + vec_diff_y * vec_diff_y), batch_type(0.)); } vec_contribution.store_unaligned(&potential[i]); } value_type result{0.}; // Loop through target data (remaining scalar part) for(std::size_t i = vec_size; i < size; ++i) { const value_type local_target_x = position_x[i], local_target_y = position_y[i]; result = 0.; // Loop through source data for(std::size_t j = 0; j < size; ++j) { if(i != j) { const value_type diff_x = local_target_x - position_x[j], diff_y = local_target_y - position_y[j]; result += charge[j] / std::sqrt(diff_x * diff_x + diff_y * diff_y); } } potential[i] = result; } }
3.2.2. Implementation on GPU using CUDA
The CUDA kernel presented here was originally extracted from ScalFMM 2.0 and was rewritten to fit the current simplified context. Before moving on, we provide the reader for brief yet comprehensive introductions to (old-fashioned) CUDA for beginners:
- Useful macro for error handling
For convenience, we define the following macro named
CHECK_CUDAto handle errors in CUDA API calls.#pragma once #include "utils.hpp" #include <concepts> #include <functional> #include <iostream> #include <type_traits> #include <cuda_runtime.h> // Error handling macro #define CHECK_CUDA(call) \ { \ cudaError_t err = call; \ if(err != cudaSuccess) \ { \ throw std::runtime_error(std::string("CUDA error at ") + __FILE__ + ":" + std::to_string(__LINE__) + \ " - " + cudaGetErrorString(err)); \ } \ }
- CUDA kernel using shared memory
3.3. Implementations using Kokkos
In this section, we present the implementations that were obtained using Kokkos. To give a general idea, Kokkos offers built-in instructions that can be used to parallelize common patterns. We focused particularly on the Kokkos::parallel_for and Kokkos::parallel_reduce instructions, which allow for quick parallelization of for loops. The Kokkos::parallel_for instruction is used to parallelize a for loop with independent iterations, while Kokkos::parallel_reduce is used to perform a reduction operation. We explored two approaches to parallelize the P2P inner with Kokkos. The first involves flat parallelism, where only one of the two loops is parallelized. The second approach employs nested and hierarchical parallelism, allowing both loops to be parallelized simultaneously.
3.3.1. Flat parallelism
- Using
parallel for
Let's dive into the code provided below. We begin by defining a set of aliases via the
usingkeyword (this is completely optional but it helps to simplify the code by avoiding to deal directly with lengthy type names). The memory space (where the data is stored) and the execution space (where the code runs) are determined at compile time, based on the chosen backend. This is controlled by a set of macros defined before the function, although Kokkos can often deduce the appropriate memory and execution spaces automatically, depending on the selected backend. Additionally, we can specify the memory layout (for example layout right or layout left, more details here), which is useful for handling multi-dimensional arrays. For optimal performance, the most efficient layout depends on the backend in use.Now let's shift our focus on the "computation part" of the kernel. This implementation uses the
Kokkos::parallel_forinstruction to parallelize the outermost loop. Note the similarity with the traditional (and notorious)#pragma omp parallel_forOpenMP directive. This instruction is used in combination with a 1D range policy used to iterate over the source particle indices (specified as the first argument of theKokkos::parallel_forinstruction). Note that the parallelized instructions (the body) are contained within a lambda function (roughly speaking, an anonymous function), although a functor could also be used (which is a class or struct that overloads theoperator()allowing instances of that class to be called as if they were functions).Kokkos uses custom containers called views to manage memory on both the host and the device. Unlike standard containers, only views can be used within a
Kokkos::parallel_forsection. Data is populated into views on the host via mirrors, and if needed, a deep copy transfers the data from the host to the device. However, if the code is set to run directly on the host, no data transfer occurs. Thus, this implementation is portable, it can run on CPUs (with OpenMP or C++ threads as backends) as well as on GPUs (using CUDA as the backend for example).#pragma once #include "utils.hpp" #include <Kokkos_Core.hpp> #include <concepts> #include <iostream> #include <type_traits> #ifdef KOKKOS_ENABLE_CUDA #define MemSpace Kokkos::CudaSpace #define ExecSpace Kokkos::Cuda #define Layout Kokkos::LayoutLeft #endif #ifdef KOKKOS_ENABLE_OPENMP #define MemSpace Kokkos::HostSpace #define ExecSpace Kokkos::OpenMP #define Layout Kokkos::LayoutRight #endif #ifdef KOKKOS_ENABLE_THREADS #define MemSpace Kokkos::HostSpace #define ExecSpace Kokkos::Threads #define Layout Kokkos::LayoutRight #endif #ifndef MemSpace #define MemSpace Kokkos::HostSpace #define ExecSpace Kokkos::DefaultHostExecutionSpace #define Layout Kokkos::LayoutRight #endif /** * @brief Portable P2P inner kernel using Kokkos parallelism (only the 'Kokkos::parallel_for' instruction). * * This function calculates pairwise interactions (potential in this case) between particles based on * their positions and charges using the 'Kokkos::parallel_for' instruction to parallelize the outermost * loop of the kernel. It enables parallel execution across different hardware architectures (e.g., CPU, * GPU), making it portable. It sets up device views, copies data between host and device, * runs the parallel computation, and retrieves the results back to the host (note that no data transfer * occurs when the code is executed directly on the host). * * @tparam ContainerType The type of container used for the positions, charges, and potentials. This container must * support random access (e.g., `std::vector`, `std::array`) and store floating-point values. * * @param[in] position_x Container of x-coordinates of the particles on the host. * @param[in] position_y Container of y-coordinates of the particles on the host. * @param[in] charge Container of charge values associated with each particle on the host. * @param[out] potential Output container where the computed potential for each particle is stored on the host. * @param[out] elapsed_time The elapsed time (in seconds) for the parallel computation. * */ template<Container ContainerType> auto p2p_inner_flat_parallel_for(ContainerType const& position_x, ContainerType const& position_y, ContainerType const& charge, ContainerType& potential, float& elapsed_time) -> void { // Set-up (aliases) using container_type = ContainerType; using value_type = typename container_type::value_type; using execution_space_type = ExecSpace; using memory_space_type = MemSpace; using layout_type = Layout; using policy_type = Kokkos::RangePolicy<execution_space_type>; using view_type = Kokkos::View<value_type*, layout_type, memory_space_type>; using host_mirror_type = typename view_type::HostMirror; using timer_type = Kokkos::Timer; #ifdef LOCAL_VERBOSITY // Print execution space details std::cout << std::string(40, '-') << '\n'; execution_space_type ex{}; std::cout << " - Execution Space = " << ex.name() << '\n'; // Print memory space details memory_space_type mem{}; std::cout << " - Memory Space = " << mem.name() << '\n'; std::cout << std::string(40, '-') << '\n'; #endif const std::size_t size = position_x.size(); // Declaration of the views view_type view_position_x("view_position_x", size); view_type view_position_y("view_position_y", size); view_type view_charge("view_charge", size); view_type view_potential("view_potential", size); // Create host mirrors of device views host_mirror_type host_position_x = Kokkos::create_mirror_view(view_position_x); host_mirror_type host_position_y = Kokkos::create_mirror_view(view_position_y); host_mirror_type host_charge = Kokkos::create_mirror_view(view_charge); host_mirror_type host_potential = Kokkos::create_mirror_view(view_potential); // Initialize vectors on host (via mirrors) for(std::size_t i = 0; i < size; ++i) { host_position_x[i] = position_x[i]; host_position_y[i] = position_y[i]; host_charge[i] = charge[i]; } // Deep copy from host mirrors to device views Kokkos::deep_copy(view_position_x, host_position_x); Kokkos::deep_copy(view_position_y, host_position_y); Kokkos::deep_copy(view_charge, host_charge); timer_type timer{}; // Actual computation Kokkos::parallel_for( "Extern for", policy_type(0, size), KOKKOS_LAMBDA(std::size_t i) { const value_type local_x_target = view_position_x(i), local_y_target = view_position_y(i); value_type result{0.}; for(std::size_t j = 0; j < i; ++j) { const value_type diff_x = view_position_x(j) - local_x_target, diff_y = view_position_y(j) - local_y_target; result += view_charge[j] / std::sqrt(diff_y * diff_y + diff_x * diff_x); } for(std::size_t j = i + 1; j < size; ++j) { const value_type diff_x = view_position_x(j) - local_x_target, diff_y = view_position_y(j) - local_y_target; result += view_charge[j] / std::sqrt(diff_y * diff_y + diff_x * diff_x); } view_potential(i) = result; }); // We make sure that everything is completed before moving on... Kokkos::fence(); elapsed_time = timer.seconds(); // Deep copy device view to host view Kokkos::deep_copy(host_potential, view_potential); // Retrieve values for(std::size_t i = 0; i < size; ++i) { potential[i] = host_potential[i]; } }
- Using
parallel reduce
We now present a second approach. Unlike the previous implementation, this version uses the
Kokkos::parallel_reduceinstruction to parallelize the innermost loop, performing a reduction on the target potential being updated. While this alternative produces correct numerical results, it is expected to have lower performance due to the reduced level of parallelism compared to the previous version (this is confirmed with the results shown in the result section). Similarly to the first approach, we use a 1D range policy to iterate over the source particle indices. Additionally, we still use views and mirrors to manage potential data transfers between the host and device as needed.#pragma once #include "utils.hpp" #include <Kokkos_Core.hpp> #include <concepts> #include <iostream> #include <type_traits> #ifdef KOKKOS_ENABLE_CUDA #define MemSpace Kokkos::CudaSpace #define ExecSpace Kokkos::Cuda #define Layout Kokkos::LayoutLeft #endif #ifdef KOKKOS_ENABLE_OPENMP #define MemSpace Kokkos::HostSpace #define ExecSpace Kokkos::OpenMP #define Layout Kokkos::LayoutRight #endif #ifdef KOKKOS_ENABLE_THREADS #define MemSpace Kokkos::HostSpace #define ExecSpace Kokkos::Threads #define Layout Kokkos::LayoutRight #endif #ifndef MemSpace #define MemSpace Kokkos::HostSpace #define ExecSpace Kokkos::DefaultHostExecutionSpace #define Layout Kokkos::LayoutRight #endif /** ,* @brief Portable P2P inner kernel using Kokkos parallelism (only the 'Kokkos::parallel_reduce' instruction). ,* ,* This function calculates pairwise interactions (potential in this case) between particles based on ,* their positions and charges using the 'Kokkos::parallel_reduce' instruction to parallelize the innermost ,* loop of the kernel. It enables parallel execution across different hardware architectures (e.g., CPU, ,* GPU), making it portable. It sets up device views, copies data between host and device, ,* runs the parallel computation, and retrieves the results back to the host (note that no data transfer ,* occurs when the code is executed directly on the host). ,* ,* @tparam ContainerType The type of container used for the positions, charges, and potentials. This container must ,* support random access (e.g., `std::vector`, `std::array`) and store floating-point values. ,* ,* @param[in] position_x Container of x-coordinates of the particles on the host. ,* @param[in] position_y Container of y-coordinates of the particles on the host. ,* @param[in] charge Container of charge values associated with each particle on the host. ,* @param[out] potential Output container where the computed potential for each particle is stored on the host. ,* @param[out] elapsed_time The elapsed time (in seconds) for the parallel computation. ,* ,*/ template<Container ContainerType> auto p2p_inner_flat_parallel_reduce(ContainerType const& position_x, ContainerType const& position_y, ContainerType const& charge, ContainerType& potential, float& elapsed_time) -> void { // Set-up (aliases) using container_type = ContainerType; using value_type = typename container_type::value_type; using execution_space_type = ExecSpace; using memory_space_type = MemSpace; using layout_type = Layout; using policy_type = Kokkos::RangePolicy<execution_space_type>; using view_type = Kokkos::View<value_type*, layout_type, memory_space_type>; using host_mirror_type = typename view_type::HostMirror; using timer_type = Kokkos::Timer; #ifdef LOCAL_VERBOSITY // Print execution space details std::cout << std::string(40, '-') << '\n'; execution_space_type ex{}; std::cout << " - Execution Space = " << ex.name() << '\n'; // Print memory space details memory_space_type mem{}; std::cout << " - Memory Space = " << mem.name() << '\n'; std::cout << std::string(40, '-') << '\n'; #endif const std::size_t size = position_x.size(); // Declaration of the views view_type view_position_x("view_position_x", size); view_type view_position_y("view_position_y", size); view_type view_charge("view_charge", size); view_type view_potential("view_potential", size); // Create host mirrors of device views host_mirror_type host_position_x = Kokkos::create_mirror_view(view_position_x); host_mirror_type host_position_y = Kokkos::create_mirror_view(view_position_y); host_mirror_type host_charge = Kokkos::create_mirror_view(view_charge); host_mirror_type host_potential = Kokkos::create_mirror_view(view_potential); // Initialize vectors on host (via mirrors) for(std::size_t i = 0; i < size; ++i) { host_position_x[i] = position_x[i]; host_position_y[i] = position_y[i]; host_charge[i] = charge[i]; } // Deep copy host mirrors to device views Kokkos::deep_copy(view_position_x, host_position_x); Kokkos::deep_copy(view_position_y, host_position_y); Kokkos::deep_copy(view_charge, host_charge); timer_type timer{}; // Actual computation for(std::size_t i = 0; i < size; ++i) { const value_type local_x_target = host_position_x(i), local_y_target = host_position_y(i); Kokkos::parallel_reduce( "Intern reduce", policy_type(0, size), KOKKOS_LAMBDA(std::size_t j, value_type& result) { if(i != j) { const value_type diff_y = view_position_y(j) - local_y_target, diff_x = view_position_x(j) - local_x_target; result += view_charge[j] / std::sqrt(diff_y * diff_y + diff_x * diff_x); } }, host_potential(i)); } // We make sure that everything is completed before moving on... Kokkos::fence(); elapsed_time = timer.seconds(); // No deep copy needed here as host_potential was directly updated // Kokkos::deep_copy( host_potential, view_potential ); // Retrieve values for(std::size_t i = 0; i < size; ++i) { potential[i] = host_potential[i]; } }
3.3.2. Nested parallelism
The two previous approaches can be categorized as flat parallelism. However, this new version of the P2P inner kernel below uses nested parallelism, which involves multiple layers of parallel execution. In practice, we combine several Kokkos instructions, such as Kokkos::parallel_for and Kokkos::parallel_reduce, to achieve this (most of the time, we expect this to lead to better results than with simple flat parallelism). While the handling of views, mirrors, and deep copies remains unchanged from the previous implementations, the "computation part" differs as both loops are now parallelized. Instead of using a simple 1D range policy, we employ a team policy that distributes the workload across the two loops. This approach distributes the threads into teams that form a league (more details here), drawing an analogy to CUDA, where all the threads are organized in a grid made up of blocks.
#pragma once #include "utils.hpp" #include <Kokkos_Core.hpp> #include <concepts> #include <iostream> #include <type_traits> #ifdef KOKKOS_ENABLE_CUDA #define MemSpace Kokkos::CudaSpace #define ExecSpace Kokkos::Cuda #define Layout Kokkos::LayoutLeft #endif #ifdef KOKKOS_ENABLE_OPENMP #define MemSpace Kokkos::HostSpace #define ExecSpace Kokkos::OpenMP #define Layout Kokkos::LayoutRight #endif #ifdef KOKKOS_ENABLE_THREADS #define MemSpace Kokkos::HostSpace #define ExecSpace Kokkos::Threads #define Layout Kokkos::LayoutRight #endif #ifndef MemSpace #define MemSpace Kokkos::HostSpace #define ExecSpace Kokkos::DefaultHostExecutionSpace #define Layout Kokkos::LayoutRight #endif /** * @brief Portable P2P inner kernel using Kokkos parallelism (both 'Kokkos::parallel_for' and 'Kokkos::parallel_reduce' instructions). * * This function calculates pairwise interactions (potential in this case) between particles based on * their positions and charges using nested parallelism via Kokkos. It combine the 'Kokkos::parallel_for' * instruction to parallelize the outermost loop and the 'Kokkos::parallel_reduce' instruction to parallelize * the innermost loop. * * @tparam ContainerType The type of container used for the positions, charges, and potentials. This container must * support random access (e.g., `std::vector`, `std::array`) and store floating-point values. * * @param[in] position_x Container of x-coordinates of the particles on the host. * @param[in] position_y Container of y-coordinates of the particles on the host. * @param[in] charge Container of charge values associated with each particle on the host. * @param[out] potential Output container where the computed potential for each particle is stored on the host. * @param[out] elapsed_time The elapsed time (in seconds) for the parallel computation. */ template<Container ContainerType> auto p2p_inner_nested_parallel(ContainerType const& position_x, ContainerType const& position_y, ContainerType const& charge, ContainerType& potential, float& elapsed_time) -> void { // Set-up (aliases) using container_type = ContainerType; using value_type = typename container_type::value_type; using execution_space_type = ExecSpace; using memory_space_type = MemSpace; using layout_type = Layout; using view_type = Kokkos::View<value_type*, layout_type, memory_space_type>; using host_mirror_type = typename view_type::HostMirror; using range_policy_type = Kokkos::TeamPolicy<execution_space_type>; using member_type = typename range_policy_type::member_type; using timer_type = Kokkos::Timer; #ifdef LOCAL_VERBOSITY // Print execution space details std::cout << std::string(40, '-') << '\n'; execution_space_type ex{}; std::cout << " - Execution Space = " << ex.name() << '\n'; // Print memory space details memory_space_type mem{}; std::cout << " - Memory Space = " << mem.name() << '\n'; std::cout << std::string(40, '-') << '\n'; #endif const std::size_t size = position_x.size(); // Declaration of the views view_type view_position_x("view_position_x", size); view_type view_position_y("view_position_y", size); view_type view_charge("view_charge", size); view_type view_potential("view_potential", size); // Create host mirrors of device views host_mirror_type host_position_x = Kokkos::create_mirror_view(view_position_x); host_mirror_type host_position_y = Kokkos::create_mirror_view(view_position_y); host_mirror_type host_charge = Kokkos::create_mirror_view(view_charge); host_mirror_type host_potential = Kokkos::create_mirror_view(view_potential); // Initialize vectors on host (via mirrors) for(std::size_t i = 0; i < size; ++i) { host_position_x[i] = position_x[i]; host_position_y[i] = position_y[i]; host_charge[i] = charge[i]; } // Deep copy host mirrors to device views Kokkos::deep_copy(view_position_x, host_position_x); Kokkos::deep_copy(view_position_y, host_position_y); Kokkos::deep_copy(view_charge, host_charge); timer_type timer{}; // Actual computation Kokkos::parallel_for( "Extern for", range_policy_type(size, Kokkos::AUTO), KOKKOS_LAMBDA(const member_type& teamMember) { const std::size_t i = teamMember.league_rank(); const value_type local_x_target = view_position_x(i), local_y_target = view_position_y(i); value_type result{0.}; Kokkos::parallel_reduce( Kokkos::TeamThreadRange(teamMember, size), [&](std::size_t j, value_type& innerUpdate) { if(i != j) { const value_type diff_y = view_position_y(j) - local_y_target, diff_x = view_position_x(j) - local_x_target; innerUpdate += view_charge[j] / std::sqrt(diff_y * diff_y + diff_x * diff_x); } }, result); Kokkos::single(Kokkos::PerTeam(teamMember), [&]() { view_potential(i) += result; }); }); // We make sure that everything is completed before moving on... Kokkos::fence(); elapsed_time = timer.seconds(); // Deep copy from device view to host mirror Kokkos::deep_copy(host_potential, view_potential); // Retrieve values for(std::size_t i = 0; i < size; ++i) { potential[i] = host_potential[i]; } }
3.3.3. Hierarchical parallelism
Finally, an attempt was made to implement what is known in the Kokkos ecosystem as hierarchical parallelism. As in the nested approach, this one combines several instructions, such as Kokkos::parallel_for and Kokkos::parallel_reduce. Likewise, instead of using a simple 1D range policy, we use a team policy to distribute the workload across several loops. As in the previous section, we use teams of threads arranged into a league, allowing for more structured parallel execution. The difference this time is that we use a shared memory space for the threads within a team, known as the team scratch pad memory, which is definitely analogous to CUDA’s shared memory. We use this scratch pad memory to cache data that can be reused during computations. Below is an example of how this feature can be used. We reorganized the computation to distribute the workload in a way that leverages the scratch pad memory. Although this version produced accurate numerical results, it did not yield a significant performance improvement over the previous implementations (see the result section), indicating that further investigation is needed, and this remains a work in progress at the time of writing.
#pragma once #include "utils.hpp" #include <Kokkos_Core.hpp> #include <concepts> #include <iostream> #include <type_traits> #ifdef KOKKOS_ENABLE_CUDA #define MemSpace Kokkos::CudaSpace #define ExecSpace Kokkos::Cuda #define Layout Kokkos::LayoutLeft #endif #ifdef KOKKOS_ENABLE_OPENMP #define MemSpace Kokkos::HostSpace #define ExecSpace Kokkos::OpenMP #define Layout Kokkos::LayoutRight #endif #ifdef KOKKOS_ENABLE_THREADS #define MemSpace Kokkos::HostSpace #define ExecSpace Kokkos::Threads #define Layout Kokkos::LayoutRight #endif #ifndef MemSpace #define MemSpace Kokkos::HostSpace #define ExecSpace Kokkos::DefaultHostExecutionSpace #define Layout Kokkos::LayoutRight #endif /** * @brief Portable P2P inner kernel using Kokkos parallelism (hierarchical parallelism). * * This function calculates pairwise interactions (potential in this case) between particles based on * their positions and charges using a hierarchical parallel execution model provided by the Kokkos library. * The computation is divided into teams of threads that process chunks of data, making use of shared * scratch memory to minimize global memory access and improve performance. The function handles data * transfer between host and device, manages synchronization, and measures the total elapsed time * for the computation. * * @tparam ContainerType The type of container used for the positions, charges, and potentials. This container must * support random access (e.g., `std::vector`, `std::array`) and store floating-point values. * * @param[in] position_x Container of x-coordinates of the particles on the host. * @param[in] position_y Container of y-coordinates of the particles on the host. * @param[in] charge Container of charge values associated with each particle on the host. * @param[out] potential Output container where the computed potential for each particle is stored on the host. * @param[in] chunk_size The size of each chunk to be processed by a team of threads. * @param[in] vec_size The vector length (to use in the hierarchical parallel execution). * @param[out] elapsed_time The elapsed time (in seconds) for the parallel computation. */ template<Container ContainerType> auto p2p_inner_hierarchical_parallel(ContainerType const& position_x, ContainerType const& position_y, ContainerType const& charge, ContainerType& potential, std::size_t chunk_size, std::size_t vec_size, float& elapsed_time) -> void { // Set-up (aliases) using container_type = ContainerType; using value_type = typename container_type::value_type; using execution_space_type = ExecSpace; using memory_space_type = MemSpace; using layout_type = Layout; using view_vector_type = Kokkos::View<value_type*, layout_type, memory_space_type>; using view_matrix_type = Kokkos::View<value_type**, layout_type, memory_space_type>; using host_mirror_type = typename view_vector_type::HostMirror; using host_mirror_matrix_type = typename view_matrix_type::HostMirror; using range_policy_type = Kokkos::TeamPolicy<execution_space_type>; using member_type = typename range_policy_type::member_type; using scratch_memory_space_type = typename execution_space_type::scratch_memory_space; using scratch_pad_view_type = Kokkos::View<value_type*, scratch_memory_space_type>; using timer_type = Kokkos::Timer; #ifdef LOCAL_VERBOSITY // Print execution space details std::cout << std::string(40, '-') << '\n'; execution_space_type ex{}; std::cout << " - Execution Space = " << ex.name() << '\n'; // Print memory space details memory_space_type mem{}; std::cout << " - Memory Space = " << mem.name() << '\n'; std::cout << std::string(40, '-') << '\n'; #endif const std::size_t size = position_x.size(); const std::size_t nb_chunks = (size + chunk_size - 1) / chunk_size; // Declaration of the views view_matrix_type view_position_x("view_position_x", chunk_size, nb_chunks); view_matrix_type view_position_y("view_position_y", chunk_size, nb_chunks); view_matrix_type view_charge("view_charge", chunk_size, nb_chunks); view_matrix_type view_potential("view_potential", size, nb_chunks); // Create host mirrors of device views host_mirror_matrix_type host_position_x = Kokkos::create_mirror_view(view_position_x); host_mirror_matrix_type host_position_y = Kokkos::create_mirror_view(view_position_y); host_mirror_matrix_type host_charge = Kokkos::create_mirror_view(view_charge); host_mirror_matrix_type host_potential = Kokkos::create_mirror_view(view_potential); // Initialize vectors on host (via mirrors) std::size_t local_index{}; for(std::size_t e = 0; e < nb_chunks; ++e) { for(std::size_t i = 0; i < chunk_size; ++i) { local_index = e * chunk_size + i; if(local_index < size) { host_position_x(i, e) = position_x[local_index]; host_position_y(i, e) = position_y[local_index]; host_charge(i, e) = charge[local_index]; } else { // Zero-padding host_position_x(i, e) = 0.; host_position_y(i, e) = 0.; host_charge(i, e) = 0.; } } } // Deep copy from host mirrors to device views Kokkos::deep_copy(view_position_x, host_position_x); Kokkos::deep_copy(view_position_y, host_position_y); Kokkos::deep_copy(view_charge, host_charge); std::size_t scratch_mem_size{3 * scratch_pad_view_type::shmem_size(chunk_size)}; timer_type timer{}; // Actual computation int level{0}; Kokkos::parallel_for( "Extern for", range_policy_type(nb_chunks, Kokkos::AUTO, vec_size).set_scratch_size(level, Kokkos::PerTeam(scratch_mem_size)), KOKKOS_LAMBDA(const member_type& team_member) { const std::size_t e = team_member.league_rank(); // Cache source data into scratch pad memory scratch_pad_view_type shared_position_x(team_member.team_scratch(level), chunk_size); scratch_pad_view_type shared_position_y(team_member.team_scratch(level), chunk_size); scratch_pad_view_type shared_charge(team_member.team_scratch(level), chunk_size); if(team_member.team_rank() == 0) { Kokkos::parallel_for(Kokkos::ThreadVectorRange(team_member, chunk_size), [&](std::size_t i) { shared_position_x(i) = view_position_x(i, e); shared_position_y(i) = view_position_y(i, e); shared_charge(i) = view_charge(i, e); }); } // Synchronization (to make sure that all the values are cached) team_member.team_barrier(); Kokkos::parallel_for(Kokkos::TeamThreadRange(team_member, size), [&](std::size_t j) { const std::size_t local_i = j % chunk_size, local_e = j / chunk_size; const value_type local_x_target = view_position_x(local_i, local_e), local_y_target = view_position_y(local_i, local_e); value_type local_result{0.}; Kokkos::parallel_reduce( Kokkos::ThreadVectorRange(team_member, chunk_size), [&](std::size_t i, value_type& update_local_result) { if(j != e * chunk_size + i && e * chunk_size + i < size) { const value_type diff_y = shared_position_y(i) - local_y_target, diff_x = shared_position_x(i) - local_x_target; update_local_result += shared_charge(i) / std::sqrt(diff_y * diff_y + diff_x * diff_x); } }, local_result); view_potential(j, e) = local_result; }); }); // Final reduction (over all the chunks) Kokkos::parallel_for( "Extern for", range_policy_type(size, Kokkos::AUTO), KOKKOS_LAMBDA(const member_type& team_member) { const std::size_t j = team_member.league_rank(); value_type result{0.}; Kokkos::parallel_reduce( Kokkos::TeamVectorRange(team_member, nb_chunks), [&](std::size_t e, value_type& inner_update) { inner_update += view_potential(j, e); }, result); Kokkos::single(Kokkos::PerTeam(team_member), [&]() { view_potential(j, 0) = result; }); }); // We make sure that everything is completed before moving on... Kokkos::fence(); elapsed_time = timer.seconds(); // Deep copy device view to host mirror Kokkos::deep_copy(host_potential, view_potential); // Retrieve values for(std::size_t j = 0; j < size; ++j) { potential[j] = host_potential(j, 0); } }
3.3.4. Vectorization with Kokkos via Kokkos SIMD
Additionally, we implemented a version that uses the Kokkos SIMD API (still experimental at the time of writing), which provides tools similar to those found in xsimd, acting as a set of wrappers for SIMD intrinsics. Unlike previous approaches, this version is designed to run only on the CPU but it is portable across different CPU architectures, though it supports fewer instruction sets compared to xsimd. This feature of Kokkos allows us to write portable vectorized code specifically for the CPU. However, during the internship, we did not manage to develop a version that could run on both the GPU and the CPU with vectorization (again this is still a work in progress). The versions presented in previous sections can run on the GPU via CUDA and on the CPU via OpenMP, for example, but not with explicit vectorization like xsimd. Nonetheless, in the next section, we demonstrate that this implementation achieved performance comparable to that of xsimd (the code is also very similar).
#pragma once #include "utils.hpp" #include <Kokkos_Core.hpp> #include <Kokkos_SIMD.hpp> #include <concepts> #include <iostream> #include <type_traits> /** * @brief P2P inner kernel using SIMD vectorization via Kokkos::simd API (still experimental * at the time of writing). * * This function calculates pairwise interactions (potential in this case) between particles based * on their positions and charges. It leverages SIMD vectorization via the SIMD API offered by Kokkos * to process multiple particles simultaneously. The function uses SIMD to handle large portions of the * data in parallel, while a scalar fallback handles any remaining particles that don't fit into a full * SIMD batch. We use SIMD batch logical masks to remove self-interactions (acting as a filter). * * @tparam ContainerType The type of container used for the positions, charges, and potentials. This container must * support random access (e.g., `std::vector`, `std::array`) and store floating-point values. * * @param[in] position_x Container of x-coordinates of the particles. * @param[in] position_y Container of y-coordinates of the particles. * @param[in] charge Container of charge values associated with each particle. * @param[out] potential Output container where the computed potential for each particle is stored. * */ template<Container ContainerType> auto p2p_inner_kokkos_simd(ContainerType const& position_x, ContainerType const& position_y, ContainerType const& charge, ContainerType& potential) -> void { // Set-up (aliases) using container_type = ContainerType; using value_type = typename container_type::value_type; using ksimd_type = Kokkos::Experimental::native_simd<value_type>; static constexpr std::size_t batch_size = ksimd_type::size(); const std::size_t size = position_x.size(); const std::size_t vec_size = size - size % batch_size; ksimd_type vec_local_x_target, vec_local_y_target, vec_contribution, vec_local_result; // Initialize logical mask ksimd_type vec_next_target_indices([](std::size_t i) { return i; }), vec_source_index; // Loop through target data (vectorized part) for(std::size_t i = 0; i < vec_size; i += batch_size, vec_next_target_indices += batch_size) { vec_local_x_target.copy_from(position_x.data() + i, Kokkos::Experimental::simd_flag_default); vec_local_y_target.copy_from(position_y.data() + i, Kokkos::Experimental::simd_flag_default); vec_contribution = 0.; // Loop through source data for(std::size_t j = 0; j < size; ++j) { const ksimd_type vec_diff_x = vec_local_x_target - position_x[j]; const ksimd_type vec_diff_y = vec_local_y_target - position_y[j]; // Apply logical mask to skip the case 'i = j' vec_source_index = j; vec_local_result = charge[j] / Kokkos::sqrt(vec_diff_x * vec_diff_x + vec_diff_y * vec_diff_y); where(vec_next_target_indices == vec_source_index, vec_local_result) = 0.0; vec_contribution += vec_local_result; } vec_contribution.copy_to(potential.data() + i, Kokkos::Experimental::simd_flag_default); } value_type result{0.}; // Loop through target data (remaining scalar part) for(std::size_t i = vec_size; i < size; ++i) { const value_type local_target_x = position_x[i], local_target_y = position_y[i]; result = 0.; // Loop through source data for(std::size_t j = 0; j < size; ++j) { if(i != j) { const value_type diff_x = local_target_x - position_x[j], diff_y = local_target_y - position_y[j]; result += charge[j] / std::sqrt(diff_x * diff_x + diff_y * diff_y); } } potential[i] = result; } }
4. Benchmarks and results
All the source codes of the internship are available in this repository. We provide a set of executables to test the different versions presented above. For executables that use Kokkos, it is important to note that they must be compiled with a Kokkos installation configured for the desired backend (e.g., CUDA, OpenMP, or C++ threads…). As briefly mentioned before, we used Guix to manage our development environments and ensure reproducibility. Since Kokkos configurations need to be set at compile time, several variants of the Kokkos package were introduced in Guix (e.g., kokkos-openmp, kokkos-cuda-a100, …). For reproducibility, we provide a dedicated channel file to leverage the guix time-machine command. Additionally, we created isolated development environments using the guix shell command combined with the --pure option that unsets existing environment variables to prevent any "collision" with external packages. Although the --container option would provide a fully isolated environment, it is not currently supported on PlaFRIM due to an outdated version of the running CentOS kernel, preventing containerization. Consequently, we only relied on the --pure option.
We present various experiments that can be run across different backends. For each binary, a list of available options can be viewed using the --help option as follows:
./excutable --help
4.1. On the CPU (using OpenMP)
First, we set-up the environment via Guix:
guix time-machine -C guix-tools/channels.scm -- shell --pure -m guix-tools/manifest-openmp.scm -- bash --norc
We get all the executables at once with these CMake commands:
rm -rf build-non-cuda && cmake --preset release-non-cuda cmake --build --preset build-non-cuda
The following command runs the naive (fully sequential) version introduced earlier to compute interactions between 1,000 randomly generated particles in single precision, with the computation repeated 5 times in a row.
build-non-cuda/bench-ref --number-runs 5 --number-of-particles 1000 --use-float --verbose
As recommended by the documentation of Kokkos, we can set the KOKKOS_PRINT_CONFIGURATION environment variable to enable verbose output and display the current configuration.
export KOKKOS_PRINT_CONFIGURATION=1
Since, we use OpenMP as a backend, we can use OMP_PROC_BIND and OMP_PLACES to control how threads are assigned to CPU cores. If these variables are not set, Kokkos will display a warning message prompting you to configure them.
export OMP_PROC_BIND=spread export OMP_PLACES=threads
We set OMP_PROC_BIND=spread to instruct the OpenMP runtime to distribute threads as evenly as possible across the available cores. Additionally, we configure OpenMP to place threads on separate hardware threads (i.e., logical cores when hyper-threading is enabled).
Finally, as usual, we can set the number of threads using OMP_NUM_THREADS, though it is recommended to use KOKKOS_NUM_THREADS instead, as it also applies to the C++ threads backend.
export KOKKOS_NUM_THREADS=2
The different versions can be run with the following commands, where the --check option compares the final numerical result with the reference result (baseline version).
build-non-cuda/bench-kokkos-flat-parallel-for --number-runs 5 --number-of-particles 1000 --use-float --verbose --check
build-non-cuda/bench-kokkos-flat-parallel-reduce --number-runs 5 --number-of-particles 1000 --use-float --verbose --check
build-non-cuda/bench-kokkos-nested-parallel --number-runs 5 --number-of-particles 1000 --use-float --verbose --check
build-non-cuda/bench-kokkos-hierarchical --number-runs 5 --number-of-particles 1000 --use-float --verbose --check
4.2. On the CPU (for vectorization)
For optimal vectorization, Guix allows packages to be marked as tunable, which is essential to fully take advantage of SIMD capabilities (as explained in the documentation). When using the --tune[=arch] option (typically --tune=native), binaries are compiled with the -march=arch flag (see x86 Options for examples), enabling them to specifically target the desired CPU architecture. Prior to the internship, the Kokkos packages available in Guix were not marked as tunable, so we created a local variant (defined in kokkos-variants.scm) to add this property, as described in the Guix reference manual. The original package is expected to be updated soon, so this custom version will no longer be necessary. As a result, we will be able to use the --tune[=arch] option directly. For example, for Intel Xeon Skylake Gold 6240 processors on Bora nodes in PlaFRIM (which support the AVX-512 instruction set), we provide a suitable manifest file that can be used as follows:
guix time-machine -C guix-tools/channels.scm -- shell --pure -m guix-tools/manifest-cpu-skylake.scm -L guix-tools/ -- bash --norc rm -rf build-non-cuda && cmake --preset release-non-cuda cmake --build --preset build-non-cuda
Once, everything is setup we can run the program using either xsmid:
build-non-cuda/bench-xsimd --number-runs 5 --number-of-particles 1000 --use-float --verbose --check
or Kokkos SIMD:
build-non-cuda/bench-kokkos-simd --number-runs 5 --number-of-particles 1000 --use-float --verbose --check
4.3. On the GPU (using CUDA)
Similarly, we can also perform experiments using CUDA as a backend. For instance, on a Sirocco node of PlaFRIM equipped with NVIDIA A100 GPUs:
guix time-machine -C guix-tools/channels.scm -- shell --pure -m guix-tools/manifest-a100.scm -- env LD_PRELOAD=/usr/lib64/libcuda.so:/usr/lib64/libnvidia-ptxjitcompiler.so bash --norc
rm -rf build-cuda && cmake --preset release-cuda
cmake --build --preset build-cuda
We can start by running the baseline CUDA version:
build-cuda/bench-cuda-shared --number-runs 5 --number-of-particles 1000 --use-float --verbose --check --threads-per-block 256
Likewise, for convenience, we set the KOKKOS_PRINT_CONFIGURATION variable to enable verbose output and display the current configuration.
export KOKKOS_PRINT_CONFIGURATION=1
As in the previous cases, the executables can be run as follows:
build-cuda/bench-kokkos-flat-parallel-for --number-runs 5 --number-of-particles 1000 --use-float --verbose --check
build-cuda/bench-kokkos-flat-parallel-reduce --number-runs 5 --number-of-particles 1000 --use-float --verbose --check
build-cuda/bench-kokkos-nested-parallel --number-runs 5 --number-of-particles 1000 --use-float --verbose --check
build-cuda/bench-kokkos-hierarchical --number-runs 5 --number-of-particles 1000 --use-float --verbose --check
4.4. Run all the experiments
Finally, we provide batch scripts to run directly all the experiments on PlaFRIM. This can be achieved using the following commands:
sbatch scripts/experiments-batch-bora-openmp.batch sbatch scripts/experiments-batch-bora-threads.batch sbatch scripts/experiments-batch-a100.batch sbatch scripts/experiments-batch-v100.batch sbatch scripts/experiments-batch-p100.batch sbatch scripts/experiments-batch-broadwell.batch sbatch scripts/experiments-batch-skylake.batch
4.5. Plots
After running all the experiments from the previous section, we provide a Python script plot-results.py to plot the results.
4.5.1. Comparison: xsimd vs Kokkos SIMD
mkdir -p img python3 scripts/plot-results.py --data-files \ results/bench-xsimd-f64-sirocco15.plafrim.cluster-experiment-skylake.txt \ results/bench-kokkos-simd-f64-sirocco15.plafrim.cluster-experiment-skylake.txt \ results/bench-xsimd-f32-sirocco15.plafrim.cluster-experiment-skylake.txt \ results/bench-kokkos-simd-f32-sirocco15.plafrim.cluster-experiment-skylake.txt \ --colors "yellowgreen" "violet" "lightgreen" "slateblue" \ --labels "xsimd (fp 64)" "kokkos simd (fp 64)" "xsimd (fp 32)" "kokkos simd (fp 32)" \ --linewidths 2 3 2 3 \ --marker d d s s \ --linestyles "-" ":" "-" ":" \ --title $'Comparison Kokkos::simd and xsimd\nIntel Xeon Skylake Gold 6240 @ 2.6 GHz [AVX512]' \ --xlabel "size (N)" \ --ylabel "time (s)" \ --xscale log \ --yscale log \ --plot-file "img/plot-simd-skylake.png"
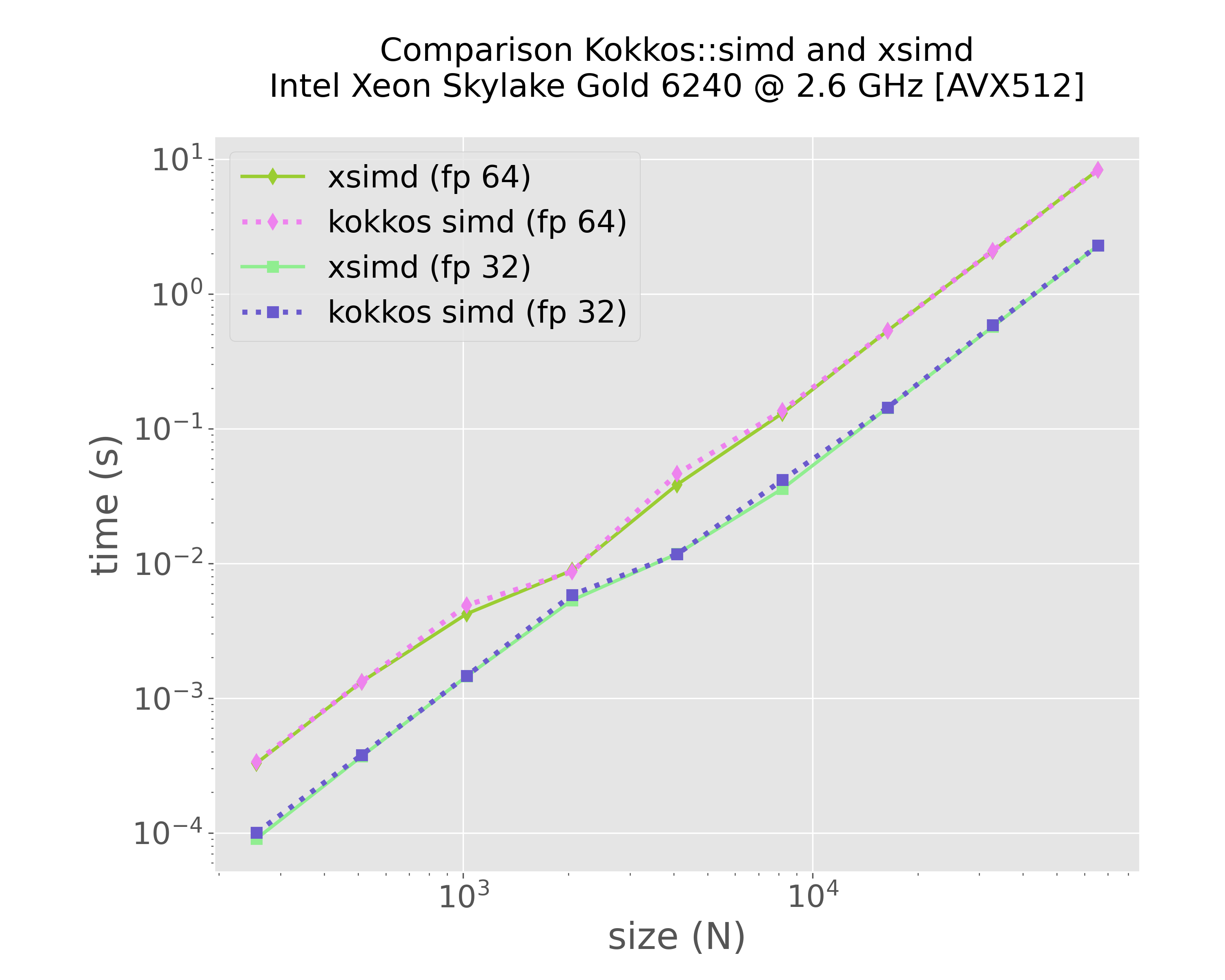
Figure 5: Comparison between xsimd and Kokkos SIMD (Intel Xeon Skylake Gold 6240)
4.5.2. Scalability (with OpenMP threads as a backend)
mkdir -p img python3 scripts/plot-results.py --data-files \ results/bench-kokkos-flat-parallel-for-openmp-time-vs-num-threads-f32-bora012.plafrim.cluster.txt \ results/bench-kokkos-flat-parallel-reduce-openmp-time-vs-num-threads-f32-bora012.plafrim.cluster.txt \ results/bench-kokkos-nested-parallel-openmp-time-vs-num-threads-f32-bora012.plafrim.cluster.txt \ results/bench-kokkos-hierarchical-openmp-time-vs-num-threads-f32-bora012.plafrim.cluster.txt \ --colors "coral" "deepskyblue" "forestgreen" "darkgoldenrod" \ --labels "Flat version (parallel_for)" "Flat version (parallel_reduce)" "Nested version" "Hierarchical version" \ --linewidths 1 1 1 1 \ --marker d s v o \ --linestyles "-" "-" "-" "-" \ --title $'Scalability with Kokkos backend = OpenMP (N=65,536)\n(2x18 core Intel Xeon Skylake Gold 6240 @ 2.6 GHz)' \ --xlabel "Number of threads" \ --ylabel "Time (s)" \ --xscale linear \ --yscale log \ --x-data 0 \ --y-data 1 \ --plot-file "img/plot-openmp-time-vs-num-threads.png"
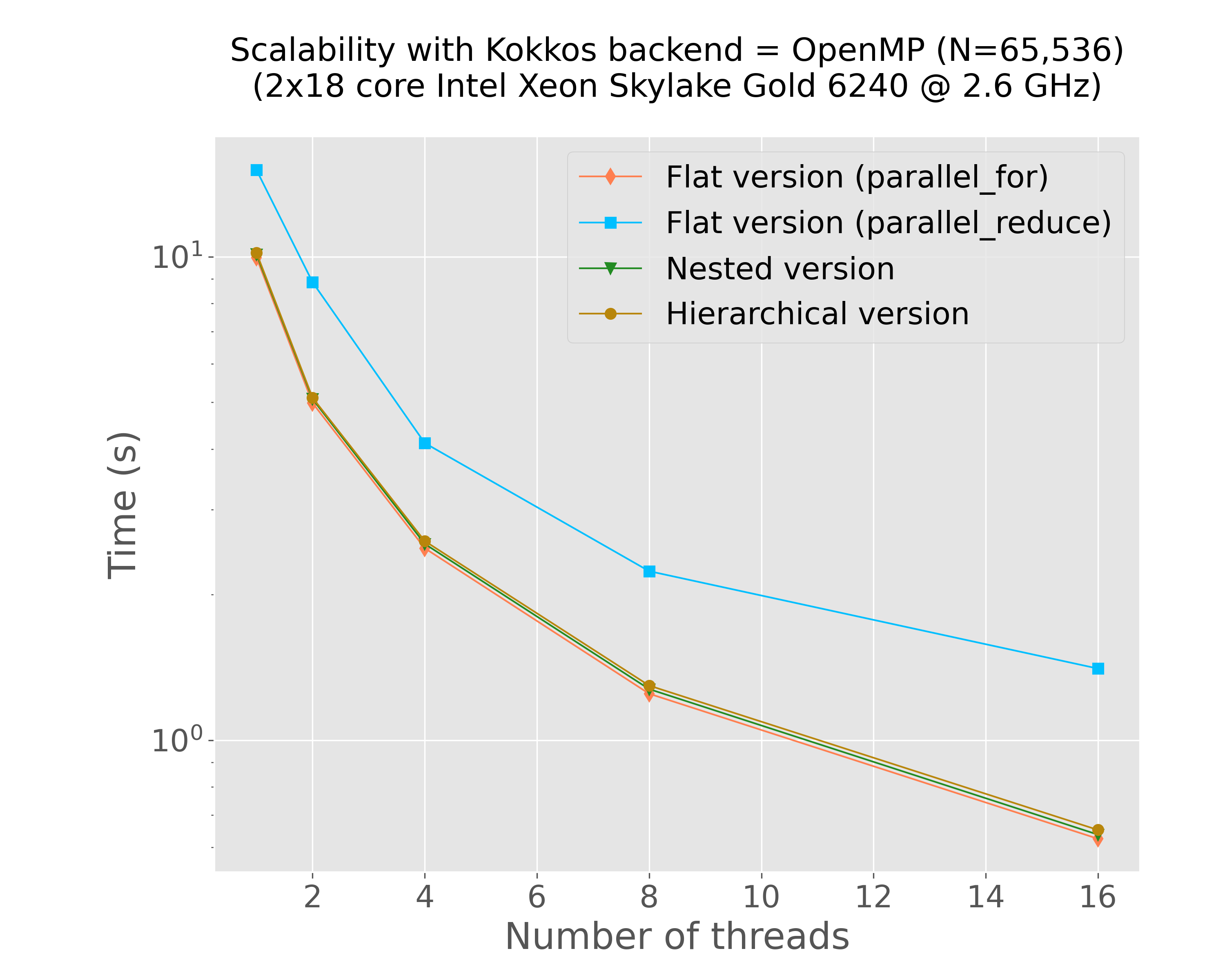
Figure 6: Strong scalability results with OpenMP (Intel Xeon Skylake Gold 6240)
4.5.3. Scalability (with C++ threads as a backend)
mkdir -p img python3 scripts/plot-results.py --data-files \ results/bench-kokkos-flat-parallel-for-threads-time-vs-num-threads-f32-bora013.plafrim.cluster.txt \ results/bench-kokkos-flat-parallel-reduce-threads-time-vs-num-threads-f32-bora013.plafrim.cluster.txt \ results/bench-kokkos-nested-parallel-threads-time-vs-num-threads-f32-bora013.plafrim.cluster.txt \ results/bench-kokkos-hierarchical-threads-time-vs-num-threads-f32-bora013.plafrim.cluster.txt \ --colors "coral" "deepskyblue" "forestgreen" "darkgoldenrod" \ --labels "Flat version (parallel_for)" "Flat version (parallel_reduce)" "Nested version" "Hierarchical version" \ --linewidths 1 1 1 1 \ --marker d s v o \ --linestyles "-" "-" "-" "-" \ --title $'Scalability with Kokkos backend = Threads (N=65,536)\n(2x18 core Intel Xeon Skylake Gold 6240 @ 2.6 GHz)' \ --xlabel "Number of threads" \ --ylabel "Time (s)" \ --xscale linear \ --yscale log \ --x-data 0 \ --y-data 1 \ --plot-file "img/plot-threads-time-vs-num-threads.png"
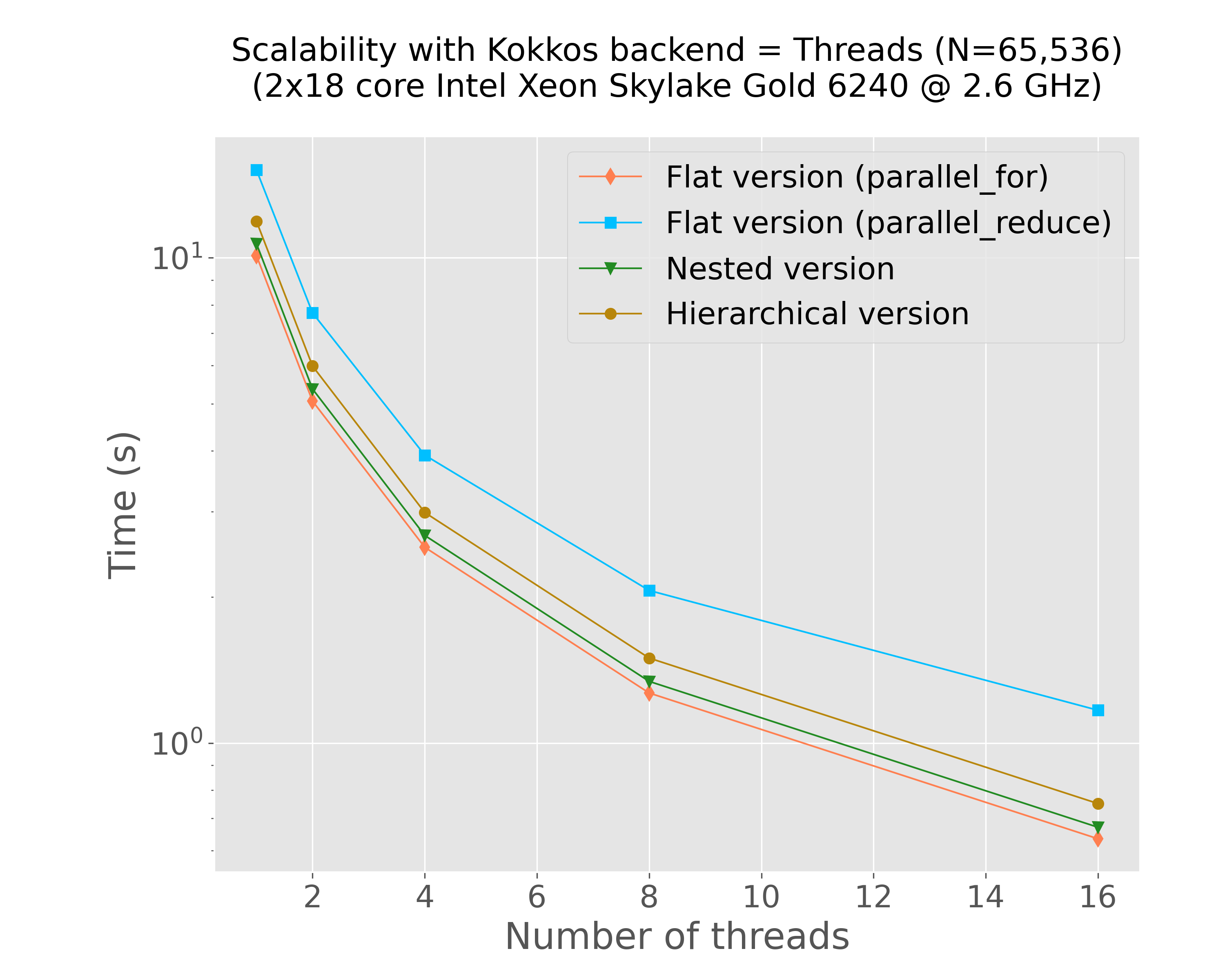
Figure 7: Strong scalability results with C++ threads (Intel Xeon Skylake Gold 6240)
4.5.4. Comparison of the strategies on the GPU (NVIDIA)
mkdir -p img python3 scripts/plot-results.py --data-files \ results/bench-kokkos-flat-parallel-for-cuda-f32-sirocco22.plafrim.cluster-experiment-a100.txt \ results/bench-kokkos-flat-parallel-reduce-cuda-f32-sirocco22.plafrim.cluster-experiment-a100.txt \ results/bench-kokkos-nested-parallel-cuda-f32-sirocco22.plafrim.cluster-experiment-a100.txt \ results/bench-kokkos-hierarchical-cuda-f32-sirocco22.plafrim.cluster-experiment-a100.txt \ results/bench-cuda-shared-f32-sirocco22.plafrim.cluster-experiment-a100.txt \ --colors "coral" "deepskyblue" "seagreen" "cyan" "red" \ --labels "Flat version (parallel_for)" "Flat version (parallel_reduce)" "Nested version" "Hierarchical version" "CUDA (reference)"\ --linewidths 2 2 2 2 1 \ --marker d s o v s\ --linestyles "-" "-" "-" "-" ":" \ --title $'Comparison of the different approaches (GPU: NVIDIA A100) [f32]' \ --xlabel "size (N)" \ --ylabel "time (s)" \ --xscale log \ --yscale log \ --plot-file "img/plot-kokkos-comparison-cuda-f32-time.png"
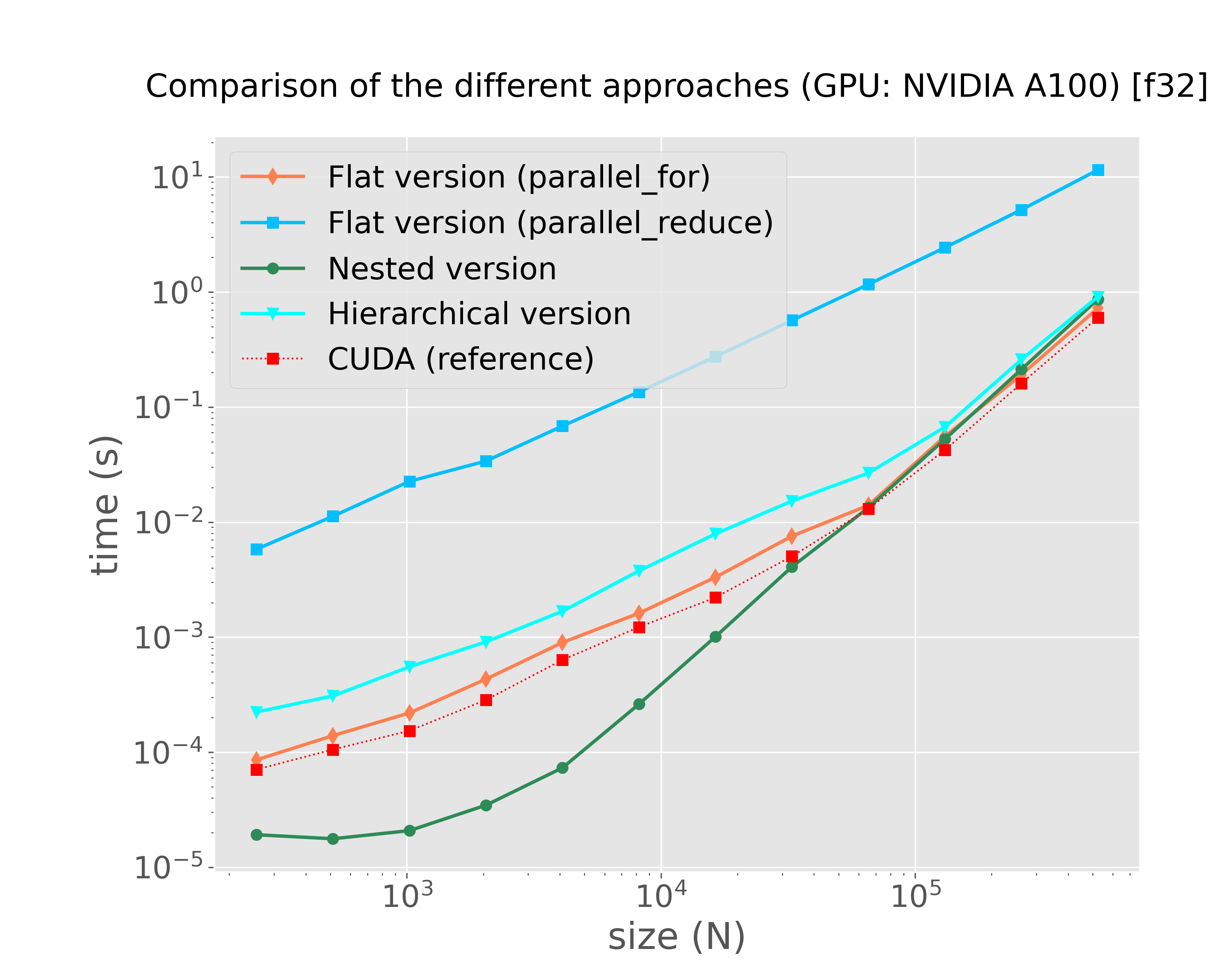
Figure 8: Comparison on GPU (NVIDIA A100)
4.5.5. Observations
In Figure 5, we can notice that both xsimd and Kokkos SIMD achieved comparable performance results on this specific kernel. The final comparison in Figure 8 indicates that the different implementations yielded results similar to those of the CUDA version. However, with the exception of the version that uses the Kokkos::parallel_reduce instruction, all other versions delivered similar performance outcomes. Given the use of the scratch pad memory, we might have expected significantly better results from the Kokkos-based hierarchical versions compared to the flat versions. This discrepancy suggests a need for further investigation, which is currently ongoing. Additionally, it would be valuable to repeat these experiments using a more complex interaction function resulting in a higher computational workload, which is also a work in progress.
5. Closing remarks
This work initially aimed to explore what Kokkos offers for writing portable code. During the project, we successfully implemented several variants of the P2P inner kernel, achieving interesting performance results. However, while the hierarchical version was expected to outperform the flat versions, this was not exactly the case. Further investigation is therefore needed to develop a more effective hierarchical approach. Moving forward, the goal is now to extend the work done for the basic electrostatic kernel to more generic kernels, allowing us to handle a wider range of interactions, such as:
\begin{equation*} k(x,y) = \frac{(x - y)}{\|x - y\|^3}, \end{equation*} \begin{equation*} k(x,y) = \ln{\bigl\{\| x - y\|\bigl\}}, \end{equation*} \begin{equation*} k(x,y) = \exp{\bigl\{\frac{- \| x - y \|}{ \sigma^2 }\bigl\}}, \end{equation*} \begin{equation*} k(x,y) = 3 \frac{(x - y) \otimes (x - y)}{\|x - y\|^5} - \frac{1}{\|x - y\|} \textbf{I}_{3 \times 3}. \end{equation*}Such work would actually provide an opportunity to explore the different possibilities offered by Kokkos views. Additionally, it's worth noting that we only tested Kokkos SIMD with a basic kernel that used common operations, and it performed comparably to state-of-the-art libraries like xsimd. It would be worthwhile to repeat these experiments with more complex kernels (involving functions like logarithmic or exponential operations, which lack pre-implemented SIMD intrinsics) to better assess the extent of support compared to other leading SIMD libraries. A future goal, as it was originally planned, would be to integrate Kokkos-based kernels into a program that uses StarPU to explore how these components can be effectively combined.